In general, statistical inference is used to draw conclusions about unknown quantities based on observed real-world data. Baysian inference is a proccess of using such data to determine unknown parameters of a probabistic model and predict new values using probability distributions as a measure of uncertainty. The process is often called model fitting.

There are multiple ways to fit a model with their own pros and contras. We will be using simulations as our method of choice because of its flexibility and relative simplicity.

Bayes' theorem¶

Bayesian inference is based on the Bayes' theorem. To understand it we should refresh our knowledge of conditional probability. According to the definition, conditional probability of the event(hypothesis) $A$ given $B$ equals to

$$ P(A \mid B) = \frac{P(A \cap B)}{P(B)} $$

where $P(A \cap B)$ is the probability that both events A and B occur. It could be useful to think about probabilities graphically:

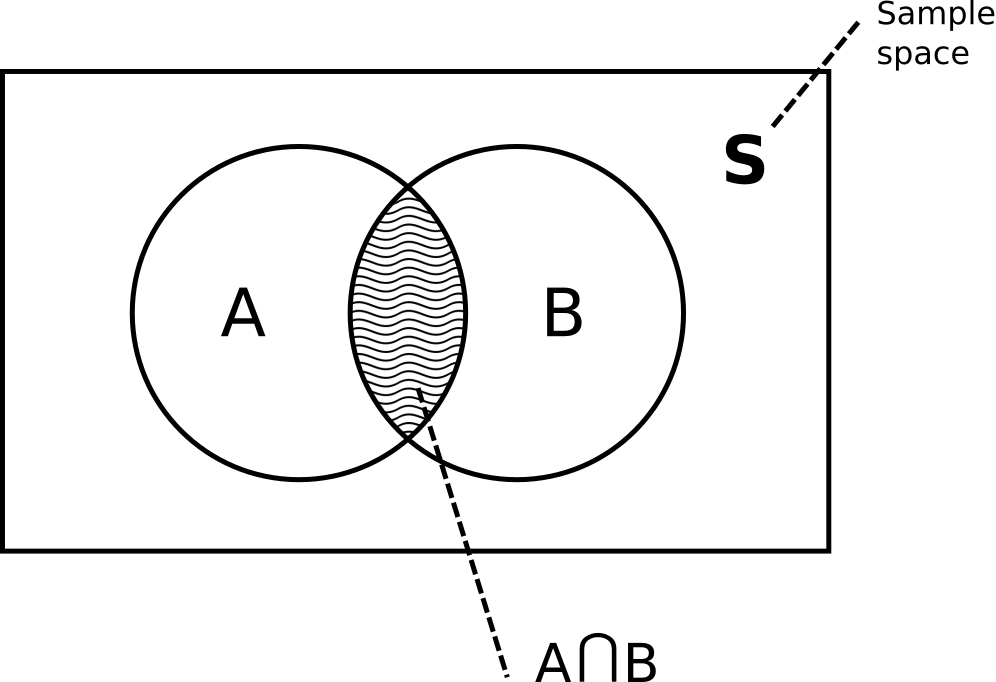
We can find conditional probability of the event $B$ given the event $A$ using the same definition:

$$ P(B \mid A) = \frac{P(B \cap A)}{P(A)} $$

Here comes the most interesting part. Knowing that $P(B \cap A)$ is equal to $P(A \cap B)$ we can combine these two formulas to get:

$$ P(A \mid B)P(B) = P(B \mid A)P(A) $$

After moving $P(B)$ to the left side of the equation we get the common form of the Bayes' theorem:

The best thing about the Bayes' theorem is the ability to get inverse conditional probability

Law of total probability¶

If we have multiple disjoint events(hypothesis) $A \tiny n$ whose union is the entire sample space, we can find a probability of any event $B$ as a sum of probabilities of all events ${A \tiny n} \cap B : n = 1,2,3,4...$ or alternatively

$$ P(B) = \sum\limits_{n} P(B \mid {A \tiny n})P({A \tiny n}) $$

Extended form of the Bayes theorem¶

Usually we don't know $P(B)$ in the Bayes' formula. Using the law of total probability we can rewrite the Bayes' formula as:

$$ P({A \tiny i} \mid B) = \frac{P(B \mid {A \tiny i})P({A \tiny i})}{\sum\limits_{n} P(B \mid {A \tiny n})P({A \tiny n})} $$

With these formulas we can already solve lots of probabilistic problems analytically (examples)

Bayesian inference¶

Using bayesian approach we can reason about unknown model parameters as random variables. In machine learning literature parameters are usually denoted as $\theta$ and $y$ denotes data. In bayesian inference, what we are interested in is the probability distribution of model parameters given observed data $p(\theta \mid y)$ or probability distribution of future data given the data we already have $p(\hat{y} \mid y)$. Using the Bayes' theorem we can find $p(\theta \mid y)$:

$$ p(\theta \mid y) = \frac{p(y \mid \theta)p(\theta)}{p(y)} $$

According to the law of total probability in discrete case $p(y) = \sum\limits_{n}p(y \mid \theta)p(\theta)$ is a sum over all possible values of the model parameter $\theta$
In case of continuous $\theta$ we have $p(y) = \int p(y \mid \theta)p(\theta)d\theta$

Where:

• $p(y)$ is prior distribution of $\theta$
• $p(y \mid \theta)$ is likelihood of the data
• $p(\theta \mid y)$ is posterior distribution we are interested in

Sometimes the factor $p(y)$ is emitted because it doesn't depend on $\theta$ so the formula becomes

$$ p(\theta \mid y) \propto p(y \mid \theta)p(\theta) $$

Where $\propto$ means "proportional to". When you design a model in StatSim, the program converts it to the probabilistic model $p(y, \theta)$ and then use different algorithms to sample from the posterior distribution $p(\theta \mid y)$

...