Conditional probability, conditional distributions, rejecting specific samples
var iframer = require('./iframer')
In previous chapters we describe how to build probabilistic models using blocks of random variables. Such models provide us a way to reason about real-life processes and events in a forward direction, starting with a random unknown input going to the results we can process and analyze. StatSim thanks to WebPPL, a probabilistic language it based on, makes it possible to reason in backward direction. Knowing something about the results, get a distribution of variables it based. Broadly speaking it's a csituation when we have partial information about the model or assume it and try to figure out distribution of still unknown quantities.
Conditional probability is one of the most important parts of probability theory. It provides us a way to reason about probabilistic models under the condition of having partial information about them.
Conditional probability¶
To understand properly what conditional probability means, we should start with 3 things:
- Sample space $\mathbb{S}$ with a total probability of $1$ is all possible outcomes experiment can have
- Two mutually inclusive events $A$ and $B$ (mutually inclusive events can overlap or in other words happen in the same time)
- Event $A \cap B$ (intersection of events, or in other words event that corresponds to both events $A$ and $B$ happening simultaniously)
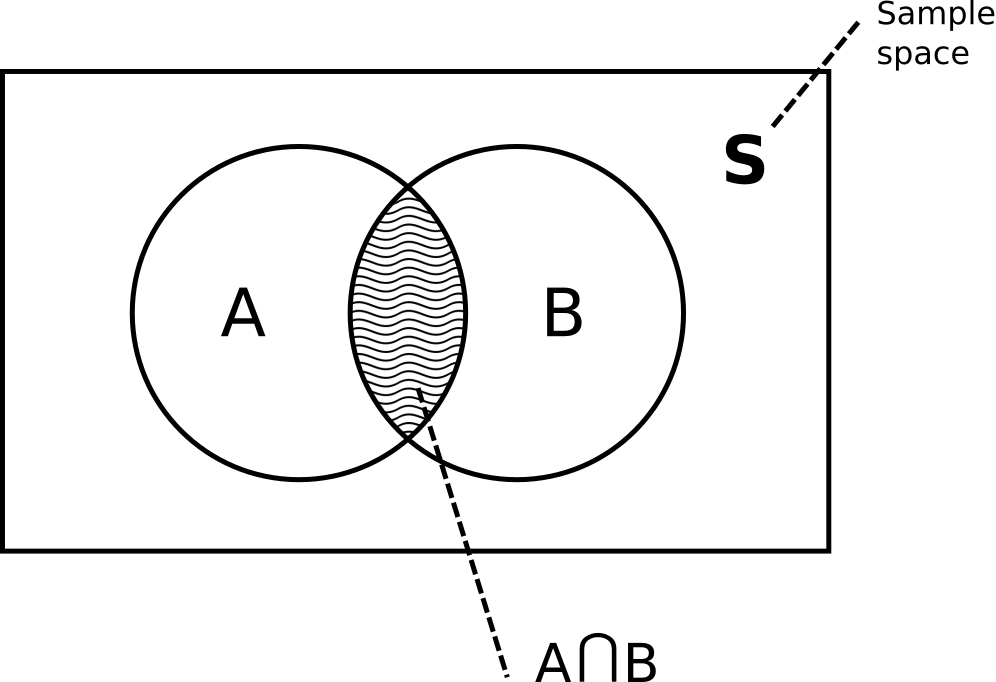
If we assume that event B already happened, it becomes our new sample space. And that part of event $B$ that used to represent the intersection of $A$ and $B$ now represent a conditional event $A \mid B$
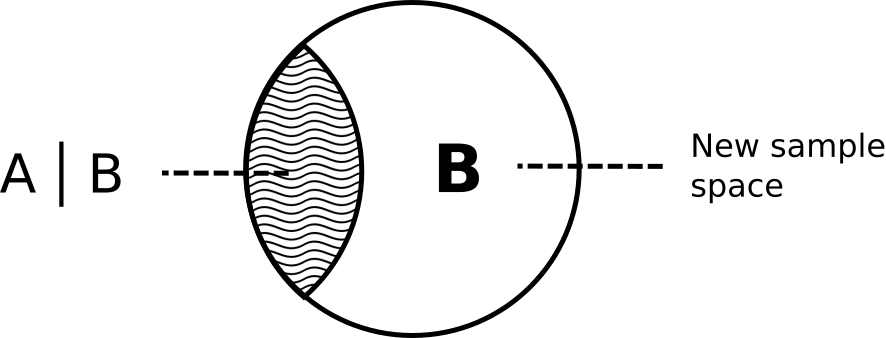
Probability of such event is defined as follows:
$$ P (A \mid B) = \frac{P(A \cap B)}{P(B)} $$If both events consist of equally likely outcomes we can think about that formula as a proportion of outcomes that fall in both events $A$ and $B$ and outcomes that fall in $B$, event we are conditioning.
Conditional distribution¶
Condition block¶
It's the simplest model block in StatSim. It only contains one input field that is used for writing conditional statements. To create a new Conditional block click New block then choose Condition
Rejection Sampling¶
Until now we used Rejection sampling algorithm to generate random samples in a forward way. We created random variables used them in the model in different ways then analyzed the output. What rejection sampling can also do is reject samples that don't satisfy the Condition blocks. It continues generating and rejecting values until the total number of successful (such that satisfy provided conditions) samples is equal to the Samples parameter of the model. Using that technique we can model conditional probability and think in backward style. If the output is equal to X what is the input.
Example: Throwing a coin 10 times¶
Binomial distribution defines a random variable that equals to number of successful (true) results of N Bernoulli random variables with the same probability of success for each variable equal to P. Let's say our experiment consists of throwing a coin 10 times and counting number of Heads. Such value is distributed according to Binomial distribution with the parameter N equal to 10. What if after performing the experiment we got 2 heads? How can we reason about the P? The point estimate can give us its value equal to 2/10 but can we trust such estimate? Let's model that!
We will create out target variable P as a uniformly distributed on the range (0,1) random variable. That variable is used as a parameter P of the Binomial distribution for the second variable ProbAmount. At that point ProbAmount will generate an output containing possible values Binomial distribution can return with all different values of P. But it's not what we are interested in. We need to condition on ProbAmount being equal to 2 and examine P. To do that add a third block Condition containing the expression ProbAmount === 2. Now, if we output ProbAmount it will show only one scalar value 2 no matter how many samples we generate. But if we add P to the output instead of ProbAmount the result will show the distribution we are interested in.
iframer('https://statsim.com/app/?a=%5B%7B%22b%22%3A%5B%7B%22d%22%3A%22Uniform%22%2C%22n%22%3A%22P%22%2C%22o%22%3Afalse%2C%22p%22%3A%7B%22a%22%3A%220%22%2C%22b%22%3A%221%22%7D%2C%22sh%22%3Atrue%2C%22t%22%3A0%2C%22dims%22%3A%221%22%7D%2C%7B%22d%22%3A%22Binomial%22%2C%22n%22%3A%22ProbAmount%22%2C%22o%22%3Afalse%2C%22p%22%3A%7B%22p%22%3A%22P%22%2C%22n%22%3A%2210%22%7D%2C%22sh%22%3Afalse%2C%22t%22%3A0%2C%22dims%22%3A%221%22%7D%2C%7B%22t%22%3A5%2C%22v%22%3A%22ProbAmount%20%3D%3D%3D%202%22%7D%5D%2C%22mod%22%3A%7B%22n%22%3A%22Main%22%2C%22e%22%3A%22%22%2C%22s%22%3A1%2C%22m%22%3A%22rejection%22%7D%2C%22met%22%3A%7B%22sm%22%3A%2210000%22%7D%7D%5D')
Conditioning on continious variables¶
It's important to understand how the rejection sampling algorithm works because sometimes it can stuck if used not correctly. Because it rejects samples until they satisfy all the condition blocks, if you create a condition that is always false, the program will freeze. That is the case when conditioning on continious variables with strong rules like A === 0.5 where A is a continious random variable. In continuous case the probability of getting one specific value is equal to 0 so rejection sampler generates thousands of values immediately rejecting them.